学部時代は一応機械工学科でした、サイトーです。
今回は機械工学科に進学したら殆ど確実に逃れられない四力の中でも、割と広汎に出てくるくせに説明が難しいことで有名な「断面二次モーメント」と「断面二次極モーメント」について書いていこうと思います。
機械工学科に進学した方は、まず四力と呼ばれる科目を取らされる取ると思います。
四力といえばこの4つです。
- 材料力学
- 流体力学
- 機械力学
- 熱力学
この4つの中で特に材料力学では断面二次モーメントとか断面二次極モーメントとかいうよく分からないワードが出てくると思います。
この記事では、そんな良くわからないワードに苦しむ機械工の学生を助けられるようにサイトーが頑張ります。
断面二次モーメントの定義式
x軸まわりの断面二次モーメントの定義式はこんな感じ。
$$I_x=\int_A y^2 dA=\int_\frac{-b}{2}^\frac{b}{2} y^2 a dy$$x軸まわりの断面二次モーメントの最終形がこんな感じになる理由を解説しますね。
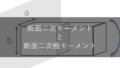
まず断面二次モーメントをやるときは四角柱を考えると思うので、状況としてはこんな柱を想像してください。

この柱の断面図がこんな感じです。

濃い青の微小面積dAを考えると
$$dA=a \times dy$$になりますよね?(横✕縦で面積)
それをyで積分するので、積分範囲を考えると断面の上端と下端の座標から
となる訳です。
「x軸まわりの」という表現は「この画像のx軸をドリルみたいに回転させた場合を考えると」って表現に変えると分かりやすいかと思います。
柱に対して考えると、柱の画像の矢印の向きに力を加えた場合です。
y軸まわりを考える場合は、断面図をこんな感じにして考えましょう。

それなので定義式を考え直すと
$$I_y=\int_A y^2 dA=\int_\frac{-a}{2}^\frac{a}{2} x^2 b dx$$となります。
断面二次極モーメントの定義式
円柱におけるz軸まわりの断面二次極モーメントの定義式はこんな感じ。
$$I_z=\int_A r^2 dA=\frac{\pi d^4}{32}$$多分、断面二次極モーメントの問題が出るのは円柱が多いと思いますので、状況としてはこんな感じで半径がdの円柱を想像してください。

この場合の断面図はこんな感じで考えます。
ちなみにz軸は画面からあなたに向かう方向が正です。

この断面図の考え方における黒の微小面積dAを考えると
$$dA=2\pi r dr$$となるので、定義式を書き直すと
$$I_z=\int_0^d r^2 2\pi r dr$$となります。
なんかもう一種類くらい導出の方法があった気がするんですがどうやったっけ…?
誰かこっそりコメント欄かお問い合わせから教えて下さい
断面二次モーメントって何?
結論から言うと、断面二次モーメントとは「モノの曲げにくさ」を表すパラメータです。
定義式を細かく見ると、距離(の絶対値)と面積の積を軸に対して平行に積分していることから、構造材の断面の任意の箇所における単位面積に対する曲げモーメントの大きさ(小ささ)を示すパラメータであることが分かると思います。
なんで二乗するの?(二次で考えるの?)
「なんで普通のモーメント(距離✕力)じゃなくて距離を二乗してるの?」ってところなんですが、これは正直あまりサイトーも分かっていません。
ただ、予想としては「通常のモーメントだと総和が0になるから」が理由だと思います。
二乗しないver.は断面一次モーメントと呼ばれますが、これは図心を求めるために用いられます。
つまり、図形上の重心を求めるためのものです。
断面二次モーメントは先述したように「単位面積に対する曲げモーメントの大きさ」を表すパラメータとしたいので、距離に負の値を取ってもらっては困る訳です。(相殺しちゃうから)
そのため、(トートロジーみたいではありますが)距離を二乗して図心からの距離を長さとして出しているのではないかと思います。
断面二次極モーメントって何?
結論から言うと、断面二次極モーメントとは「モノのねじりにくさ」を表すパラメータです。
これも定義式を細かく見ていくと、距離(の絶対値)と面積の積を軸に対して放射状に積分していることから、構造材の 断面の任意の箇所における単位面積に対すねじりモーメントの大きさ(小ささ)を示すパラメータであることが分かると思います。
まとめ
これまでをまとめるとこんな感じになります。
- 断面二次モーメントはモノの曲げにくさを示すパラメータ
- 断面二次極モーメントはモノのねじりにくさを示すパラメータ
- つまり断面二次と断面二次極では表現したいパラメータが違う
- モーメントを二乗する理由は多分距離を絶対値で置きたいから
- 通常のモーメントで考えると中立面に対してモーメントの総和が0になる
定義式を見てすぐに「あ~なるほどね」となった方は少ないと思います。
かく言うサイトーもggっては「?」となることを繰り返しておりました。
安心してください。こんなポンコツでもちゃんと学部は卒業できました…
ただ、この「断面二次モーメント」と「断面二次極モーメント」ですが、材料力学以外の四力でも割と出てきますし、なんだったら四力以外の部分でも出てきます。
それなので、今のうちにしっかりとイメージを固めておいておくようにしてください。








コメント